数学は暗記です
数学が苦手な方の多くは、ある誤解をしています。何かといいますと、
「数学は考えるもの」
「単に覚えるだけの社会に比べて面倒臭い」
少なくとも受験数学は、「考える」よりも「覚える」が大事です。そしてその学習法は本来の数学よりも「受験英語」が近いといえます。
暗記ってどうやれば上手くいく?
暗記というのは面倒な作業です。単純に文字の羅列を覚えようとしても、なかなか覚えられません。

例えば社会科の場合、イメージで覚えるのが最も効率的です。
ある歴史上の人物を名前だけで覚えようとせず、例えば歴史漫画に出てくるキャラクターとして、絵で覚えている。単に男性か女性かというだけでなく、例えば「太っている」「背が高い」あるいは「馬に乗っている」「軍服を着ている」といった感じです。
他にも年号を覚える場合、単に数字だけを覚えるのではなく「語呂合わせ」を用いたりします。また、ある出来事が別の出来事よりも前か後かを知っているだけで、正確な年号を覚えていなくても正解できるケースも存在します。これは漫画のみならず、例えば時代劇や大河ドラマのシーンから思い出したりすること等が考えられます。
即ち、社会科は暗記科目ですが、同時に暗記をする方法が確立されている科目だともいえるわけです。
余談ですが中国における文官の登用試験で世界的にも最難度といわれる「科挙」は主に古典(四書五経)の暗記でした。
これをどのように覚えたかといいますと、「文章をイメージ化する」という方法です。即ち、ある文節を暗記しようとした場合、単に書いて覚えたり、あるいは暗唱するのではなく、その文章のシーンをビジュアルで表現できるよう頭の中でイメージする。そうすることで自然と文章が思い出せるようになるという方法が多く用いられていたといいます。
数学の定理や公式はどうやれば暗記できるか?
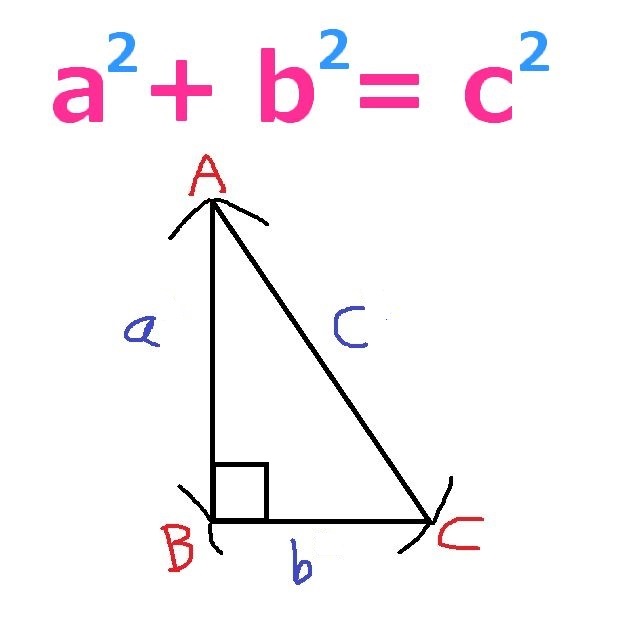
数学の定理や公式を暗記が難しいのは、このようなビジュアル化の方法が確立されていないのが問題です。即ち、単なる文字や図形の羅列を丸暗記するのは「非常に難しい」。
頭の中で瞬時に計算が出来るとか、あるいは図形の特徴を一瞬で把握する、いわば「建築家の才能がある」といった、特殊な人は除いて多くの方が「暗記できない」のです。
言い換えれば、このような人と同じ方法で暗記をしてはいけない。加えて社会科のようなビジュアル化が出来れば「暗記は可能」ということになります。そしてこの方法に当たるのが「地図を用いる」という方法です。
目的地にどれだけ早く到達できるか?
三角形ABCがあるとします。目的地をCとした場合、A地点よりもB地点からの方が近い。ここまでは何となく分かるでしょう。
では、この三角形が直角三角形である場合、どのくらい距離が違うのか…
おそらく多くの方はこのように思われるかもしれません。
「それが分かったからといって一体何になるんだ?」
実は、歴史においてはこの問題が非常に重要な要素となっています。何かといいますと、
距離の計算は合戦において最も重要な情報の一つ
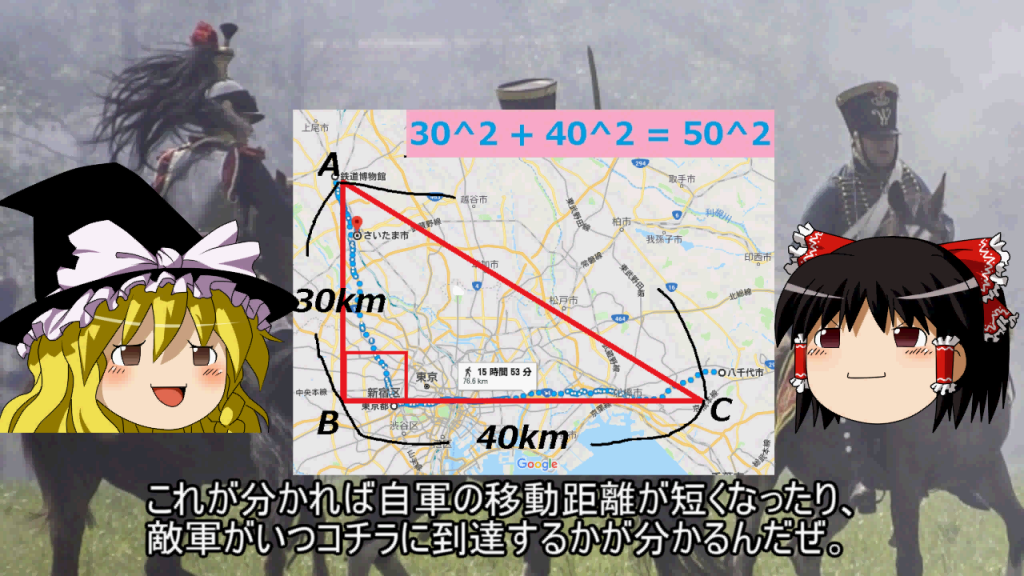
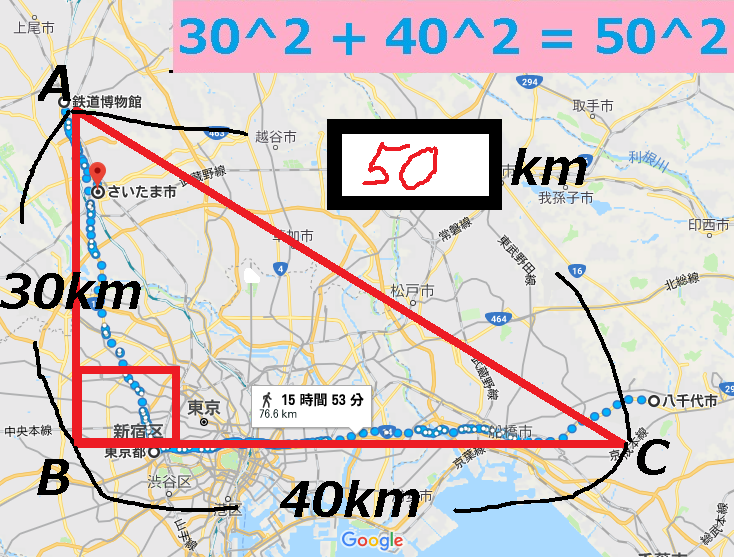
だからです。例えば上記の画像にある三角形において、B地点からC地点に向かった部隊と、同じくA地点から向かった場合、スタート地点から目的地までの到達距離が10km違うとします。
もし仮に、一日で行軍出来る距離が10km未満だとした場合、先に目的地に到達した部隊は1日の休憩が可能ということになります。なぜなら「相手の部隊は1日では到達できない」という事が分かっているため、安心して休憩がとれるわけです。
逆に、そのような状態を想定し、強行軍で1日以内に目的地に到達する。そして休憩中の部隊に対して「奇襲攻撃」を仕掛けるというシナリオも存在します。
これは数学の定理の一つである「三平方の定理」を理解していることで、そのような歴史上の合戦を分析することが可能なわけです。そうすることで、今までは単に歴史上の出来事としてしか捉えていなかった合戦を、あたかもリアルタイムで進行している、あるいはその戦いを中継するかの如く見る事が出来ます。
また、このような「数学的な」事実を把握することで、史実とは逆の展開を想定し、小論文やレポートの作成に用いることも可能となるわけです。
ブログ、あるいは創作物にも使える「数学的発想」とは?
例えば地図を眺め、ある目的地に「より近く」辿り着く方法。あるいは「敢えて時間をかけて」辿り着く方法を予想し、実際に目的地まで歩いて検証してみる。これだけでブログを書き続ける事が可能です。
あるいは小説等の創作物においても、このような数学的発想は大いに役立ちます。
「あの合戦は、この方法なら別の結果になっていたのでは?」
例えば味方が裏切ったとか、あるいは特定の武将が活躍したという話だけでなく「行軍速度」といった視点から検証をしてみる。その内容を基に小説を書くこと等も可能なわけです。
このような方法を用いるのは、単にクリエイティブというだけではありません。常日頃から数学的な発想で物事を考えるようになるため、その考えを用いた際に思い出した数学の定理や公式を嫌でも思いだすようになる。したがって、
忘れない
のです。言い換えれば「アウトプットの習慣が根付く」といったところでしょうか。
動画でも解説致しております↓↓